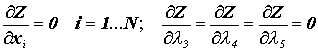Итак мы имеем:

m = (4,5 , 14,4 , –3,5 , –10,4 , 0,01 , 0,02 , 0,1 , 0,08)

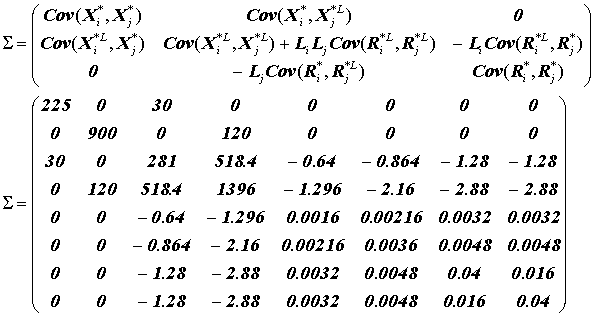
Решением без ограничений является:
x = cS^–1 m = ( 1 , 0,8 , –0,23 , –0,18 , –568,1 , 245,1 , 94,8 , 54,4 )^Т

Которое, однако, не является допустимым, поскольку оно требует занятия короткой позиции по двум рискам резервов убытков и выпуска коротких облигаций на сумму 568,1 денежных единиц. При наличии ограничений данная оптимизационная задача будет выглядеть так:

c x^T m – x^TS ^–1 x ® max   ; x₃ = x₄ = x₅ = 0.

Z = c x^T m – x^T S^–1 x + l₃ x₃ + l₄ x₄ + l₅ x₅ ® max

Где l₃ , l₄ , l₅ – Лагранжевы множители ассоциированные с указанными ограничениями. Чтобы решить задачу при данных ограничениях нам нужно найти вектор x₁ , … , x_N   ( N = 2m+n) такой, что

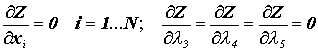
А это эквивалентно системе линейных уравнений:

– m_i c + 2 S_j=1…N s_{i j} x_j – S_j=3…5 l_j s_{i j} = 0
x₃ = x₄ = x₅ = 0.

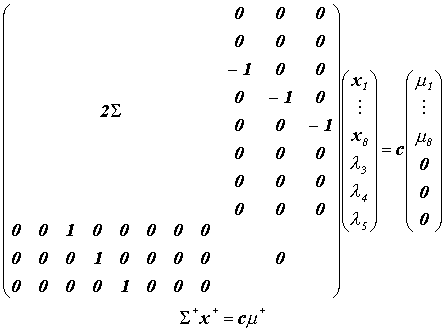
А ее решение есть: x⁺ = c (S ⁺)^–1 m⁺. Таким образом оптимальный портфель с ограничениями будет следующий:

Андеррайтинговый риск.	Коэффициент a , b или А	Ожидаемая прибыль	Вклад в общую дисперсию
–X*1 + l1 + E X*1	1	4.5	225
–X*2 + l2 + E X*2	0,8	11,52	576
Риск резервов убытков
–X*1L + l1L – (R*1L – r0 )L1	0	0	0
–X*2L + l2L – (R*2L – r0 )L2	0	0	0
Риски активов
R*1 – r0	0	0	0
R*2 – r0	82,3	1,65	82,3
R*3 – r0	94,14	9,41	470,68
R*4 – r0	52,47	4,2	209,88
Всего		31,28	1563,86

Оптимальный размер капитала составит u = t^–1 V / R, где R и V суть ожидаемая прибыль и вклад в общую дисперсию соответственно (см. секцию 2.2.). Сделав такое же предположение о величине t мы получаем u = 199,98.

Легко заметить следующие важные свойства оптимального портфеля:

• Компания передает в перестрахование 20% от своего индустриального портфеля;
• Компания полностью перестраховывает свои риски резервов убытков. Как следствие ее финансовый рычаг равен 0. И пассив баланса состоит только из собственного капитала.
• Общая величина чистых инвестированных активов составляет 228,91, в то время как капитал – только 199,98. Поэтому оптимальный портфель достижим только в случае, если компания возьмет в долг 28,93 денежных единицы по безрисковой ставке.
• Компания инвестирует существенную часть своего инвестиционного портфеля в акции и недвижимость (64%), как следствие вклад рисков активов в избыточную прибыль и общую дисперсию велик (49%)
• Оптимальное соотношение “риск – доход” равно 0,791.
• Для рисков не подпадающих под ограничения (т.е. для всех переменных кроме x₃ , x₄ и x₅ ) отношение “ожидаемая прибыль – вклад в общую дисперсию” одинаково и равно 2%. Для рисков подпадающих под ограничения это равенство не верно.