|
Библиотека Инструменты Все Страховщики Рейтинги Доп.Инфо Законодательство Ссылки. Советы Магазин Написать
|
Пример 2.
Базируясь на результатах секции, где рассматривался риск резервов убытков, наша модель предполагает, что надбавки li и liL пропорциональны
дисперсиям соответствующих рисков s2(X*i) и s2(X*iL ). На практике,
однако, передача в перестрахование всего портфеля неоплаченных убытков (bi = 0) требует гораздо более высокой надбавки. И поскольку не существует ликвидного рынка для
отдельного перестрахования рисков резервов убытков, мы делаем следующее
Предположение 7.
Число рисков резервов убытков равно числу андеррайтинговых рисков и ai = bi .
В дополнение мы упростим систему обозначений: X*i + X*iL заменим на X*i ; а li +
liL заменим на li. Теперь наша модель будет выглядеть так:
D*u – r0 u = Si=1…m ai
(EX*i + li – X*i – (R*iL –r0) Li) +
Sj=1…n (R*j –r0 )Aj
А теперь мы вновь проанализируем предыдущий пример. Итак мы имеем:
| Страховой портфель | Риск | L | l | s | l /s |
| Частные лица | X*1 | 400 | 5 | 17,61 | 28% |
| Предприятия | X*1 | 600 | 16 | 35,12 | 45% |
Остальные параметры остаются без изменений и поэтому
m = (1 , 4 , 0,01 , 0,02 , 0,1 , 0,08)
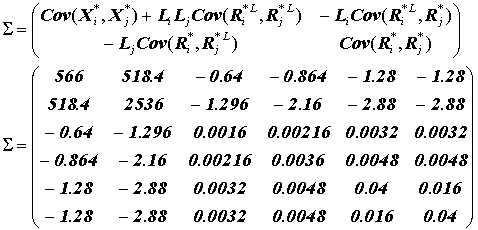
Решением без ограничений будет:
x = c S –1 m = ( 1 , 0,8 , –208,7 , 935,3 , 121,2 , 69,6 )T
которое подразумевает короткую позицию на 208,7 денежных единиц по среднесрочным облигациям (в добавление к 400 денежным единицам резерва убытков, имеющим ту же доходность, т.к. R*1L
= R*1). В условиях нашей модели такое решение не является допустимым. Поэтому мы введем дополнительное ограничение : x3 = 0. И в результате получим такую целевую функцию:
Z = c xT m – xT S–1 x + l3 x3
® max
Продифференцировав эту функцию по всем xi и по l3 мы получим следующее матричное уравнение:
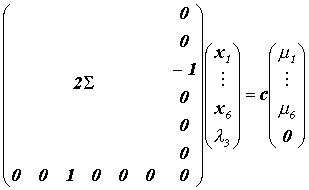
Которое достаточно легко можно решить и получить такой оптимальный при наличии ограничений портфель:
| Страховой риск | Коэффициент ai | L | Ожидаемая прибыль | Вклад в дисперсию |
| –X*1 + l1 – (R*1L – r0 )L1 | 1 | 400 | 1 | 57,95 |
| –X*2 + l2 – (R*2L – r0 )L2 | 0,75 | 450 | 2,99 | 173,35 |
| Всего | | 850 | | |
| Риски активов | Объем инвестиций Aj | | |
| R*1 – r0 | 0 | 0 | 0 |
| R*2 – r0 | 776,2 | 15,52 | 899,64 |
| R*3 – r0 | 112,1 | 11,21 | 649,5 |
| R*4 – r0 | 63,8 | 5,1 | 295,7 |
| Всего | 952,1 | 35,82 | 2076,14 |
Предполагая t = 0,25, получим, что оптимальное значение капитала u = t–1 V / R = 231,83 .
Оптимальный портфель имеет следующие важные свойства:
- В квотное перестрахование передается 25% “индустриального” портфеля.
- Компания сохраняет большую часть своих резервов ( 850 денежных единиц из 1000 брутто-перестрахование ), что означает возникновение существенного финансового рычага.
- Общий объем чистых инвестированных активов (102,1) меньше, чем оптимальный капитал (231,83). Что делает оптимальный портфель достижимым без дополнительных заимствований.
- Вклад рисков активов в общую дополнительную прибыль и в общую дисперсию значительно выше чем вклад страховых рисков ( 89% против 11% ). Это в частности связано с тем фактом, что короткая позиция по риску кривой
доходности действует как хеджирование.
- Оптимальное соотношение “риск – доход” составляет 0,786.
- Для рисков, не подпадающих под ограничения, соотношение “ожидаемая прибыль – вклад в общую дисперсию”
одинаково и равно 1,7%.
|

