Пример.
Предположим, что существует два некоррелированных риска, приносящих прибыль l₁ и l₂ , и имеющих стандартное отклонение s₁ и s₂, соответственно. Введем следующие обозначения: l_i = l_i / u и t_i = s_i / u .

Мы имеем:

m_a (u) = a ₁ l₁ + a₂ l₂
s_a² (u) = a₁² t₁² + a₂² t₂²

Цель:   2t m_a (u) – s_a² (u) ® max; {a : a₁, a₂ Î [0, 1]}

Что ведет к следующему безусловному оптимуму: a_i = t l_i / t_i².

Без потери общности рассуждения мы можем считать l₁ / t₁² ³ l₂ / t₂² и мы можем выделить следующие случаи:

1. t < t₁² / l₁ .
   В этом случае a₁ и a₂ те же что и выше и
   m_a = t ( l₁ / t₁² + l₂ / t₂² )     и     s _a² = t² ( l₁² / t₁² + l₂² / t₂² )
   поэтому (m_a , s_a ) пробегает прямую линию по мере изменения t.
2. t Î [ t₁² / l₁ , t₂² / l₂ ].
   В этом случае a₁ = 1, а a₂ = l₂ / t₂² , поэтому m_a = l₁ + t l₂ / t₂² и s_a² = s₁² + t² l₂²/ t₂², и (m_a , s_a ) оказывается гиперболой.
3. t > t₁² / l₂.
   Здесь a₁ = a₂ = 1 и m_a = l₁ + l₂, a s_a² = s₁² + s₂². Эта часть эффективной границы превращается в точку.

Теперь мы разрешим капиталу компании меняться. Мы имеем: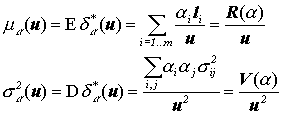

Где s²_{i j} = Cov(X_i^* , X_j^* ).
Таким образом, если Р -- точка на эффективной границе, определенная как написано выше, т.е. при фиксированном значении капитала, то любая точна на прямой 0Р может быть достигнута за счет соответствующего выбора величины капитала u. Поэтому естественно начинать оптимизационный процесс с выполнения следующего требования:

1. R(a)/V^0.5(a) = max     a : a_i Î [0, 1]
   Данное требование означает максимизацию соотношения “доход – риск”, или в терминах финансового экономикса отношения Шарпа. В общем, данное соотношение максимизируется на некотором множестве приемлемых значений a. Обозначим это множество B. Достаточно разумно, тогда, установить дополнительное требование:
   S _1…m a_i l_i = max_{a ÎB}
   Этим мы максимизируем ожидаемую прибыль нетто-перестрахование. Пусть a_М – вектор собственных удержаний, для которых выполнены оба условия. Пусть R = R(a_M) и V = V(a_M) . Тогда оптимальный капитал компании определяется следующим условием:
2. 2t R/u – V/u² = max_u
   Что означает, что оптимальным будет капитал u = t^–1 VR^–1.

1. Хотя представленный метод основывается на той же целевой функции, что и предложенный Markowitz'ем метод “среднее – дисперсия”, существует однако важные различия между двумя методами. Во-первых, оптимизируемый портфель состоит из страховых рисков, а не из финансовых активов. (В дальнейшем мы будем оптимизировать комбинированный портфель состоящий и из страховых, и из финансовых рисков.) Это ведет к тому, что наборы ограничений в двух моделях различны. В частности общее инвестиционное ограничение ( Sa_i = 1) бессмысленно и было отброшено. Во-вторых, в дополнение к оптимизации структуры портфеля компания может принять решение, о том сколько капитала ей нужно для продолжения бизнеса. Дополнительная степень свободы ведет к тому, что эффективная граница имеет другой вид, чем в модели, созданной Markowitz'ем.
2. Один из недостатков данного метода заключается в том, что в нем используется только два первых момента распределений рисков, входящих в портфель. В случае страховых рисков имеющих существенную асимметрию и растянутость это оказывается серьезным ограничением. Тем не менее в оставшейся части этой секции мы будем продолжать использовать этот метод при анализе некоторых оптимизационных задач в страховании. Нам кажется, что проведенная параллель между страхованием и финансами интересна, несмотря на указанные ограничения. В нашей общей модели, которая будет введена в секции 4, мы будем оптимизировать объединенный портфель, состоящих из страховых рисков и рискованных финансовых активов. Поскольку страховые риски входят в портфель нетто-перестрахование, не имеет смысла предполагать, что распределение доходов близко к нормальному.