
Библиотеку
 | Вернуться в Библиотеку | Содержание | << 4 >> |
|
Библиотека
|
Модель бесконечно коротких рисков.Будем называть риск бесконечно коротким, если моменты заключения и окончания договора страхования отличаются на бесконечно малую величину. При рассмотрении договоров страхования имеющих ненулевую продолжительность проявятся следующие их свойства:
Рассмотрим модель: Пусть срок действия договора перестрахования 1 год; год при этом принимается за 1 времени.
Перестрахователь заключает nдоговоров страхования в год, причем заключение договоров происходит равномерно.
p –вероятность страхового случая. M – собственное удержание перестрахователя. Пусть
введены функции: R(h) -- доля договоров с суммой, S, меньшей,
чем hSmax, причем Smax зависит от времени
заключения договора страхования, t : 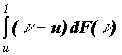 где u задается уравнением: где u задается уравнением:
Мат. ожидание выплат по этим договорам за данное время 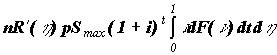 и и 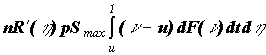 для перестрахователя и перестраховщика соответственно.
Интегрируя от 0 до 1 по dt и от 0 до 1 по dh получим мат.
ожидание выплат перестрахователя, ELx, и перстраховщика, ELy : для перестрахователя и перестраховщика соответственно.
Интегрируя от 0 до 1 по dt и от 0 до 1 по dh получим мат.
ожидание выплат перестрахователя, ELx, и перстраховщика, ELy :
При нахождении оценок ELx и ELy предлагается использовать распределения, являющиеся
смесью степенного полиномиального распределения и постоянных величин выплат, непротиворечащие выборочным функциям распределения
доли выплат и доли договоров. Т.е. предлагается представить функции F(n) и
R(h) в виде: |