Теперь, если добавить в набор допустимых инвестиций безрисковые облигации с доходностью r_f, то, поскольку этот актив имеет нулевую дисперсию и нулевую ковариацию с другими активами, каждый инвестор сможет выиграть от введения этого актива в свой инвестиционный портфель. В этом случае действует “теорема одного фонда” : “Существует такой эффективный портфель рисковых активов M, что каждый эффективный портфель есть линейная комбинация М и безрискового актива.” Это также можно видеть на рисунке 6. Линия, именуемая линией рынка капиталов, (CML, capital market line) задается уравнением:

r = r_f + s( r_M – r_f ) / s_M

На рис. 6 тонкая кривая – эффективная граница до появления безрисковых облигаций. Любая точка ( r , s ) на СML может быть получена путем инвестирования доли a = ( s_M – s ) / s_M в безрисковые облигации и доли 1 – а в портфель М. CML везде лежит выше исходной эффективной границы, кроме точки М, где эти линии совпадают. В этом случае инвесторы обязательно предпочтут точки лежащие на CML (Причем это произойдет независимо от того полон рынок или нет.). Luenberger показал, как определить веса активов соответствующие портфелю М , который мы будем называть рыночным портфелем.

Теперь мы введем в наш портфель ILS, обозначенную С, имеющую высокую ожидаемую доходность и, соответственно, большую дисперсию, но при этом имеющую незначительную корреляцию с другими рискованными активами. С, например, может быть катастрофической облигацией. По крайней мере в случае, когда облигация подвержена только риску нанесения вреда застрахованному имуществу в результате катастрофического события, имеется доказательство того, что доход имеет нулевую корреляцию с рыночным портфелем, М см. [5, 13]. Итак, новый актив имеет параметры риска и дохода s_С и r_C, а также корреляцию с рыночным портфелем r_{C, M} = Cov ( C, M ) / (s_С s_M ), которая относительно невелика.

Доход портфеля, включающего ILS, может быть представлен в виде линейной комбинации R_C и R_M :

Что соответствует точке ( s_a , r_a ) на графике, где r_a = a r_M + (1 – a) r_C и

s² _a = a² s² _M + 2a(1 – a) r_{C, M} s_С s_M + (1 – a)² s² _C

Жирная кривая на рисунке 7 есть график параметрического выражения для точек { ( s_a , r_a ) | 0 £ a £ 1 } для случая, когда s_С > s_M и m _С > m_M . Представляемые ниже аргументы докажут, что пока r_{C, M} < s_M /s_С кривая, соединяющая точки С и М будет иметь отрицательный наклон в точке М, и, следовательно она обязательно пересечет CML. Как следствие, новая CML, определенная после того, как инвесторы смогут включить в свои портфели ILS, должна иметь больший наклон, чем исходная. Это означает, что все инвесторы смогут выиграть.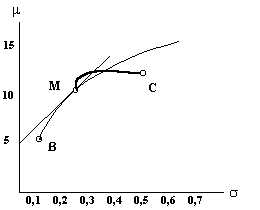

Чтобы в точке М кривая уходила влево от CML достаточно, чтобы наклон кривой в этой точке был отрицателен. Наклон можно рассчитать следующим образом:

В точке М, где а = 1, мы получим, что производная s по а равна s_M – r_{C, M} s_С.

В случае показанном на рисунке 7, r_M < r_C , поэтому наклон кривой отрицателен только при r_{C, M} < s_M /s_С. Мы считаем, что этот случай соответствует ситуации наблюдаемой на рынке катастрофических облигаций в настоящее время. Корреляция при этом не обязана быть нулевой; но все инвесторы выигрывают от появления ILS на финансовом рынке.

В случае r_M > r_C появление новых ценных бумаг также расширяет возможности инвесторов, при выполнении того же условия r_{C, M} < s_M /s_С. Наш вывод заключается в том, что появление на рынке ценной бумаги с неотрицательным относительно небольшим коэффициентом корреляции с рыночным портфелем (или с любой отрицательной корреляцией) приведет к тому, что на рынке установится новое состояние равновесия, при котором все инвесторы смогут выиграть по сравнению с исходным состоянием.

Итак, мы показали, чтобы условия инвестирования улучшились, достаточно, чтобы ковариация между доходом от новой ценной бумаги и доходом от существующих активов была относительно мала по абсолютному значению или отрицательна. Например, возможно, что долгосрочные облигации с купоном, зависящим от индекса смертности, также улучшат условия инвестирования, несмотря на то, что риск и доход у них ниже чем на рынке акций. Таким образом модель “среднее – дисперсия” дает рациональное обоснование спроса на ILS. При этом все инвесторы будут стремиться иметь портфель лежащий на новой CML, вне зависимости от их рисковых предпочтений. Страховая пресса пишет, что инвесторам нравятся новые ценные бумаги. Некоторые их выпуски характеризовались как переподписанные. А такое поведение как раз и соответствует нашей модели.

В нашем построении мы считали, что у исходного набора их п рисковых активов матрица ковариаций обратима, т.е. никакой актив не является линейной комбинации остальных. Мы предполагали, что транзакционные издержки отсутствуют, а вся информация доходит до инвесторов незамедлительно и в полном объеме; а также все другие виды несовершенства рынка, например налоги, отсутствуют. Мы называем это совершенным рынком.

В обычной конструкции, исходные п рисковых активов содержат специфические риски фирм, которые встраиваются в катастрофические облигации при их создании. Эти риски, как это обычно предполагается, можно диверсифицировать без всяких затрат. При наличии предположений по поводу транзакционных издержек, информации, и т.д. полученное равновесие не может быть изменено введением катастрофических облигаций или других подобных ценных бумаг. Их появление не изменит CML.

Наш аргумент – на реальном несовершенном рынке, появление таких ценных бумаг ведет к росту его эффективности. Их появление позволяет инвесторам конструировать нужные им портфели с меньшими затратами. Более эффективное распределение капитала по рискам приведет к тому, что на рынке сложится новое состояние равновесия, при котором все инвесторы окажутся в выигрыше.

Наша конструкция была создана, чтобы показать, что добавление таких ценных бумаг приближает рынок к состоянию равновесия, соответствующему совершенному рынку. Это происходит благодаря тому, что увеличивается PV прибылей фирм путем увеличения их активности в секторах экономики, куда инвесторы не имеют прямого доступа (роста эффективности фирм); упаковки (объединения) рисков, которые изначально были распределены по некоторым из п исходных видов ценных бумаг; и выпуска их на рынок таким образом, что инвесторы могут распределить капитал эффективнее, чем когда эти риски были распределены по исходным ценным бумагам (по причине того, что увеличилась эффективность, ибо уменьшился спрэд между ценами спроса и предложения, уменьшились затраты на информацию, и т.д. и т.п.)

Мы доказали, что существует экономическая основа для секьюритизации рисков, и, соответственно, такая деятельность может продолжаться на финансовых рынках, до тех пор, пока секьюритизация увеличивает эффективность.