2. Секьюритизация катастрофического риска.

Мы представим идеализированную иллюстрацию катастрофических облигаций. (cat bonds) В течение 1997 и 1998 годов были удачно размещены несколько видов катастрофических облигаций следующими фирмами: USAA, Swiss Re, Winterthur, St. Paul Re и другими. Ниже мы представим экономическое обоснование для предложения (почему страховщики предлагают такие бумаги) и спроса (почему инвесторы покупают их). А сейчас мы обратимся к механизму сделки.

Мы проиллюстрируем модель двумя примерами: однопериодической моделью и двухпериодической моделью. В обоих случаях катастрофический риск имеет биномиальную структуру. Ни в одном из примеров не будет риска процентной ставки. Предположим, что рыночная процентная ставка на безрисковые ц.б. является постоянной и равной 8% годовых. Вероятность катастрофы, которая вызовет неоплату долга (дефолт, хотя с юридической точки зрения это не есть дефолт, ибо и эмитент и держатель бумаг знают, в каком случае долг не будет оплачен) составляет 3% за год. Эти значения приведены просто для иллюстрации механизма сделки. В практической деятельности мы должны использовать преобладающую временную структуру процентных ставок, и некоторую модель для страховых выплат, чтобы определить вероятность. Embrechts & Meister использовали этот подход, чтобы разработать модель для оценки страховых опционов.
 

Пример 1. Этот пример аналогичен облигациям, выпущенным USAA. Номинал равен 100, купон – 12% годовых. Риску подвержены и основной долг и купон. Это значит, что и купон и номинал будут выплачены, только если никаких катастроф не произойдет в течение периода [0,1]. В этом случае купон и номинал (112) будут выплачены в момент 1. Возможность катастроф, их вероятность, вместе с финансовыми потоками от катастрофических облигаций показаны на Рисунке 1. Положительный поток – выплаты держателям бумаг; отрицательный – их плата за приобретение прав на будущие финансовые потоки.

Ожидаемая величина выплат, которую получит держатель облигации равна, С(1) = 112*0,97 + 0*0,03 = 108,64. Дисконтируя эту величину, используя процентную ставку 8%, получаем начальную цену катастрофической облигации:

108,64 / 1,08 = 100,59

А теперь предположим, что другая облигация дает гарантированный финансовый поток 112. Цена такой облигации выпущенной и погашенной в те же моменты времени, что и катастрофическая составит (рассчитываем дисконтированный финансовый поток):

112 / 108 = 103,70

Предположим, что страховщик (такой как USAA) выпускает катастрофические облигации и в тот же момент покупает обычные облигации. Обычные облигации более дорогие. Затраты страховщика на такую сделку составят 3,11 за каждые 100 единиц номинала, без учета тразакционных издержек. Что же страховщик получает в результате? Если катастрофа не произойдет, то финансовый поток для страховщика будет равен нулю, ибо то, что он выплатит при погашении катастрофических облигаций, он получит от погашения обычных. Однако, если катастрофа случится, то он все равно получит 112 (купон и номинал) при погашении простых облигаций, но ничего не выплатит по катастрофическим бумагам. В результате страховщик получает однолетний договор катастрофического перестрахования, по которому он получает 112 в случае катастрофы. Это позволяет ему увеличить объем предлагаемых страховых услуг в течение этого года (так же как при традиционном перестраховании) на 112 при затратах 3,11 на каждые 100 единиц номинала выпускаемых облигаций. Перестраховочный тариф для такого синтетического перестрахования равен 100*3,11 / 112 = 2,78 на 100 единиц (пере)страховой суммы. Чистые инансовые потоки для страховщика показаны на Рисунке 2.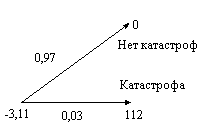

Существуют также многопериодические катастрофические облигации. Большинство из них можно считать просто ежегодными повторениями примера 1, когда дефолт происходит если произошла катастрофа, независимо от того в каком периоде катастрофа имела место. В условиях выпуска облигаций может быть прописано, что купоны и номинал не выплачиваются с того момента, когда произошла катастрофа. Другим вариантом катастрофических бумаг будет такой, когда риску подвержены только купонные выплаты и часть номинала. На самом деле USAA выпустила одну серию бумаг, где риску подвержен только купон, и одну, где – купон и основной долг. Облигации Swiss Re [20] и Yasuda Marine [29] имеют одинаковую долю номинала подверженную риску в разные годы. Облигации Winterthur имеют изменяемую (по воле фирмы) каждый год долю номинала подверженную риску. Наш второй пример – аналог облигаций Winterthur выпущенных в 1997 году [2].
 

Пример 2. Только купон подвержен риску. Номинал 100 выплачивается держателю бумаг в момент времени 2 с вероятностью 1. Купон величиной 12 выплачивается в моменты времени k = 1 и k = 2, при условии, что за промежуток времени [k – 1, k] не произошло никаких катастроф. Состояние катастроф и вероятности вместе с финансовыми потоками от катастрофической облигации приведены на рисунке 3. Положительные потоки – выплаты держателям облигаций; отрицательные – их плата за получение прав на будущие финансовые потоки.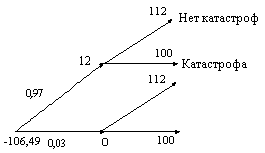

Как и в первом примере ожидаемые платежи держателям облигаций составят: С(1) = 12*0,97 = 11,64; а С(2) = 100 + 11,64 = 111,64. Дисконтированное значение ожидаемых платежей есть стоимость катастр. облигации:

1,08^-1 ( 11,64 + 111,64 * 1,08^-1 ) = 106,49

А теперь рассмотрим такую же облигацию, но безрисковую. Цена такой облигации на момент выпуска катастрофической облигации составит:

1,08^-1 ( 12 + 112 * 1,08^-1 ) = 107,13

Предположим, что как и ранее страховщик выпускает катастрофические облигации и при этом покупает обыкновенные. Сделка будет стоить страховщику 0,64 на каждые 100 единиц номинала, и обеспечивать 12 единиц перестраховочной защиты в каждом из периодов. Перестраховой “тариф” составит 100 * 0,64 / 12 = 5,33; однако нужно помнить, что “перестраховочная премия” платится в начале двухлетнего периода действия защиты, даваемой катастрофическими облигациями. Если мы желаем сравнить с ценами на защиту, даваемую однолетними облигациями, то “тариф” нужно делить на 2. В каждый из двух будущих периодов, если катастроф не случится, финансовый поток для страховщика будет нулевым, ибо он получает купон по обычным облигациям и выплачивает такой же купон по катастрофическим. Однако, если катастрофа происходит, то страховщик все равно получает купон по обычным облигациям (12), но не выплачивает купон по катастрофическим. В результате, он получает перестраховой контракт, который приносит ему 12, если катастрофа произойдет в любой из периодов. Это увеличивает возможности страховщика продавать страховые услуги в течении двух лет на 12 единиц по цене 0,64 за 100 единиц номинала ILS (или за 5,33 единовременной премии за 100 единиц защиты) Финансовые потоки для страховщика показаны на рисунке 4.

Оба рассмотренных нами примера позволяют страховщику увеличит свои возможности по предоставлению страховых услуг. Технология необходимая для выпуска ILS в настоящее время развиваются и улучшаются; и таким образом транзакционные издержки этих сделок вероятно будут со временем снижаться. Более того, ILS становятся более привычны инвесторам, что приведет к дополнительному снижению стоимости подобных сделок. И наконец, как отмечено в [13], для страховой отрасли 50 млрд. USD весьма чувствительная потеря, в то время как финансовый рынок перенесет такую потерю относительно легко. Катастрофические облигации могут стать стандартным методом перераспределения катастрофического риска. И практический анализ и экономическая теория предсказывают возможность такого исхода.

Нужно бы отметить, что для финансового рынка не важен вид страхования, это может быть и не катастрофический риск. Мы покажем ниже, что у инвесторов возникнет спрос на эти облигации по той причине, что их доходы слабо коррелируют с рынком акций. Могут быть и другие виды страхового риска имеющие слабую корреляцию с рынком акций. Например, в 1997 актуарии Winterthur предложили выпустить облигации, перераспределяющие риск смертности. Интуитивно понятно, что риск смертности имеет низкую ковариацию с финансовыми рисками, и поэтому можно предположить, что такие облигации будут привлекательны для инвесторов. Как мы знаем, Winterthur имеет долгосрочные аннуитетные пассивы, и в результате подвержен риску неожиданного уменьшения смертности бенефициариев. ILS, в которых финансовые потоки держателей бумаг привязаны к индексу смертности обеспечили бы Winterthur сверхдолгосрочной защитой, которую невозможно получить через традиционный перестраховой рынок. В США некоторые компании на сверхконкурентном рынке предлагают привлекательные полисы страхования жизни для выбранных страхователей. Нельзя сказать, что для этих групп страхователей будут действовать те же законы смертности, что и для генеральной совокупности. Секьюритизация позволит создать сверхдолгосрочную защиту от риска того, что генеральная смертность будет сильно отличаться от смертности для этих избранных групп.