На главную страницу
Вернуться в
Библиотеку		 Содержание<< 6 >>
Библиотека

Инструменты

Все Страховщики

Рейтинги

Доп.Инфо

Законодательство

Ссылки.

Советы

Магазин

Написать
 

 

 Теперь рассмотрим степенное распределение n ( т.е. F(n) = nk+1 ) при h = const = W. Согласно формуле (1) получим :
(7)

При нахождении ELy необходимо ввести A – момент времени, в который величина u ( заданная уравнением: uSmax (1+i)t W = M ) становится равной 1 т.е. . Возможны 3 варианта:

  1. При A і :: ELy = 0;
  2. При 0 Ј A < 1 ::
    (8)
  3. При A < 0
    (9)

Теперь мы можем рассмотреть последний случай: и доля выплат в сумме договора, и доля договоров с суммой меньшей или равной hSmax имеют степенное распределение: F(n) = nk+1 и R(h) = hs+1.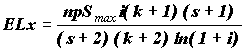
Интегрируя (7) по dh от 0 до 1, заменив W на (1+i)s+1 hs+1 получим :

При нахождении ELy, также необходимо рассматривать двa h : G такое, что для договора с h равным G величина A должна быть равна 1 ( Smax G(1+i) = M ); и H такое, что для договора с h равным H величина A должна быть равна 0 ( Smax G = M ).
Так как при h < G   A > 1, то ELy = 0; при G < h < H   0 < A < 1, то для нахождения ELy мы будем интегрировать формулу (8) по dh от G до H, заменяя W на (s+1) hs+1 ; а при h > H   A < 0 и мы будем интегрировать формулу (9) по dh от H до 1, так же заменяя W.
Возможны варианты:
  1. При G і 1 :: ELy = 0;
  2. При G < 1 ; H і 1 ::


    		(10)

ВвБ | Ind << 6 >>