|
Библиотека Инструменты Все Страховщики Рейтинги Доп.Инфо Законодательство Ссылки. Советы Магазин Написать
|
Предварительные замечания:- В нижерассматриваемых моделях будет предполагаться, что инфляция
будет сохраняться постоянной между моментами заключения первого договора, по которому могут произойти выплаты после
момента вступления договора перестрахования в силу (начало года), и моментом окончания договора перестрахования (конец
года);
- Перестраховывается эксцедент убытка по всем убыткам произошедшим за срок действия договора перестрахования;
- Год будет повсюду приниматься за 1 времени; за нуль времени будет приниматься начало года, для которого
производятся вычисления цены перестрахования;
- Предполагается, что количество договоров страхования, заключаемых
за некоторый промежуток времени зависит только от его продолжительности;
- По договору страхования возможна лишь
одна выплата, после выплаты договор страхования утрачивает силу;
- Продолжительность всех договоров страхования
одинакова;
- Моменты выплаты и страхового случая различаться не будут;
- Не будет рассматриваться вопрос
о дисконтировании, хотя, если перестраховочная премия передается перестраховщику до вступления договора перестрахования в
силу, то правильнее было бы обратиться к дисконтированным ожидаемым величинам выплат перестрахователя и перестраховщика,
но и подход не рассматривающий дисконтирования имеет право на существование, например, если перестраховщику передается
часть премии, полученной перестрахователем по некоторому договору страхования, при вступлении этого договора страхования
в силу, то правильнее использовать не дисконтированные ожидаемые выплаты.
- Степенное распределение порядка k -- распределение, задаваемое функцией распределения вида
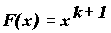 при х О [0; 1]. Полиномиальное (степенное)
распределение порядка N есть распределение, задаваемое следующей функцией распределения : при х О [0; 1]. Полиномиальное (степенное)
распределение порядка N есть распределение, задаваемое следующей функцией распределения : 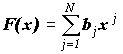 при х О [0; 1], а Сумма всех
bj должна быть равная 1. Полиномиальное распределение будет использовано ниже для
аппроксимации распределений случайных величин, принимающих значение в промежутке от нуля до единицы. при х О [0; 1], а Сумма всех
bj должна быть равная 1. Полиномиальное распределение будет использовано ниже для
аппроксимации распределений случайных величин, принимающих значение в промежутке от нуля до единицы.
Наиболее прост расчет “равнонадбавочной” цены перестрахования в случае, когда инфляция сохраняется постоянной всегда.
Пусть i темп инфляции в течении всего периода наблюдений; T -- продолжительность
каждого договора страхования . Рассмотрим 2 договора перестрахования заключенных на срок в 1 год: договор А заключен
в момент времени -1, а договор Б в момент 0. Пусть по договору
А установлено собственное удержание M/(1+i), а по договору Б -- M.
Рассмотрим величину убытков перестрахователя, ELx, и перестраховщика, ELy. Возьмем два
момента времени t: t О [0; 1] и t - 1.
Рассмотрим два договора страхования В и Г, заключенные в моменты времени 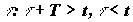 и t - 1 соответсвенно; и имеющие страховые суммы SB и
SГ, причем и t - 1 соответсвенно; и имеющие страховые суммы SB и
SГ, причем
SB = SГ (1 + i).
Вероятности
того, что страховой случай по договору В произойдет в промежуток времени [t; t + dt] и того, что
страховой случай по договору Г произойдет в промежуток времени [t - 1; t + dt -1] равны. За промежуток
времени dt выплаты перестрахователя по двум договорам составят:
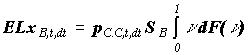 и и
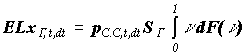 , ,
а выплаты перестраховщика:
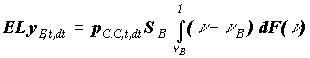 и и
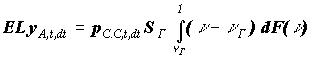
Где F(n) -- функция распределения доли
убытка в страховой сумме;
nВ = SВ/M -- величина
доли убытка в страховой сумме В такая, что, если доля убытка в сумме договора превзойдет nB, то наступает ответственность перестраховщика;
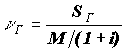 -- аналог nB для договора Г. -- аналог nB для договора Г.
Можно заметить, что
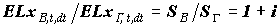 и и 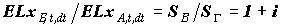 . .
Так, как величины выплат перстрахователя
и перестраховщика возрастают в одинаковое количество раз, то равнонадбавочная цена перестрахования не изменяется. Этим можно
воспользоваться при расчете цены перестрахования по вновь заключаемому договору перестрахования с собственным удержанием
М при всегда постоянной инфляции i, рассчитав по имеющимся статистическим данным цену
перестрахования за прошлый год с собственным удержанием М/(1 + i); за позапрошлый год --
М/(1 + i)2 и т. д.
|

