Сравнение моделей

Рассмотрим основные недостатки моделей для которых выведены аналитические формулы. Для модели бесконечно коротких рисков основными недостатками являются:

1. игнорирование эффектов связанных с ненулевой продолжительностью договоров страхования;
2. игнорирование возможности связи между отношением S/S_max и величиной выплачиваемой доли от суммы договора;
3. игнорирование зависимости между вероятностью страхового случая и суммой договора.

1. игнорирование зависимости между вероятностью страхового случая и суммой договора;
2. если распределение отношения S/S_max изменилось (например из-за изменения политики страховой компании ) по сравнению с прошлыми периодами, то изменение функции распределения S/S_max спрогнозировать проще, чем изменение функции распределения величины доли выплаты от max. выплаты.

Обсудим вопрос о применимости модели бесконечно коротких рисков. Хотя, бесконечно коротких рисков в природе не существует, существуют достаточно короткие договоры страхования, для которых оценка ELy, даваемая формулами (5) – (11), будет достаточно точной. Уровень "достаточной" точности устанавливается лицом, принимающим решения, но точность лучше, чем 5 - 10 % получить достаточно сложно.

Используя бесконечно короткие риски, можно получить оценку ELy сверху и оценку ELy снизу для портфеля из рисков равной продолжительности. Пусть перестрахователь заключает n договоров страхования за год, причем все договоры имеют равную продолжительность T; вероятность страхового случая по любому договору – p. Пусть, как и ранее, определены функции распределения: R(h) -- ф.р. отношенияS/S_max (t) и F(n) -- ф.р. доли выплаты в сумме договора. Рассмотрим промежуток времени [t; t + dt]. Мат. ожидание количества завершившихся договоров совпадает с количеством заключенных: ndt, и если с вероятностью
1 – (1 – p)^T происходит страховой случай, то количество таковых за данное время составит (1 – (1 – p)^T) ndt. Пусть за данный промежуток времени произошел страховой случай по договору заключенному в момент времени t, с суммой hS_max(t). Тогда ожидаемая выплата по д. договору составит

Причем правая часть этого неравенства соответствует формуле для определения мат. ожидания в случае бесконечно коротких рисков. А для перестраховщика выплата составит:

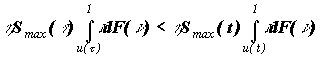
причем 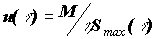больше, чем . Так как интегрирование по dR и dt сохранит неравенство, то мы получим оценку для ELy и ELx сверху. Т.е. мы получим оценку, используя формулы для бесконечно коротких рисков. Рассуждая подобным образом, мы можем получить и оценку снизу, заменяя S_max(t) на . Т.е. оценка снизу получится, если в формулах для модели бесконечно коротких рисков заменить S_max на S_max (1+i)^T. Причем, если мы будем оценивать ELy/ELx, то оценка будет лучше, чем при оценивании ELy т.к. исчезнет неточность вносимая заменой S_max(t), а останется лишь неточность от замены u(t).