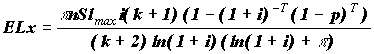(20).

При выводе формул для нахождения ELy мы введем параметры:
A такое, что A Sl_max (1+i) = M;
B такое, что B Sl_max (1+i)^{1 - T} = M;
C такое, что C Sl_max = M;
D такое, что D Sl_max (1+i)^-T = M.
Эти параметры имеют следующий смысл :
A есть такое n, чтоZ для данного n равен 1 и при n Ј A параметр Z > 1 и ELy = 0;
для n, соответствующего B, Z = 1 - T, и, следовательно, для A < n Ј B при вычислении ELy нужно использовать (16);
для n, соответствующего C, Z = 0; и для B < n Ј C нужно использовать (17);
для n, соответствующего D, Z = -T, а значит для С < n Ј D при вычислении ELy нужно использовать (18), а при n > D нужно использовать (19).

Из сказанного следуют пять возможных частных случаев:

1. A і 1 в данном случае ELy = 0;
2. A < 1 ; B і 1. Для нахождения ELy интегрируем (16) по dn от A до 1;
3. A < 1 ; B < 1 ; C і 1. В этом случае ELy есть сумма двух интегралов: от (16) по dn от A до B и от (17) по dn от B до 1;
4. A < 1 ; B < 1 ; C < 1 ; D і 1. В этом случае ELy есть сумма трёх интегралов: от (16) по dn от A до B, от (17) по dn от B до C и от (18) по dn от C до 1;
5. A < 1 ; B < 1 ; C < 1 ; D < 1. B этом случае ELy есть сумма четырех интегралов: от (16) по dn от A до B, от (17) по dn от B до C, от (18) по dn от C до D, от (19) по dn от D до 1.