
Библиотеку
 | Вернуться в Библиотеку | Содержание | << 4 >> |
|
Библиотека
|
6. Алгоритм решения задачи. Решение задачи, поставленной в секции 5, будет дано в форме итеративного алгоритма, использующего непараметрическую аппроксимацию и инверсию алгоритма Lemaire.Шаг 0. Инициализация. Берем некоторую начальную оценку для c. Выбираем параметрическую аппроксимацию для распределения случайной переменной Z.Шаг 1. Уточнение распределения величины убытка. Мы используем среднее оптимальное удержание с в качестве цензурирующей величины, чтобы определить новую оценку для вектора параметров распределения Z. Поэтому мы максимизируем функцию правдоподобия:
Шаг 2. Корректировка частоты страховых случаев. С точки зрения непараметрической аппроксимации у нас есть r классов страхователей. Для каждого из них, напомним, у нас есть:j – наблюдаемая частота убытков, полученная при непараметрической аппроксимации распределения по данным наблюдений. lj’ – реальная частота. lj” – оптимальная частота, полученная при использовании алгоритма Lemaire.Тогда можно записать: lj = plj’+(1–p) lj” (2) lj – наши наблюдения; lj’ – входные данные для алгоритма Lemaire; а lj” – результат работы этого алгоритма.Мы применили схему проб и ошибок по отношению к lj’, так чтобы наблюдения совпали с тем, что дает выражение (2). Для вектора lj’ алгоритм Lemaire дает оптимальную политику поведения cj . Тогда среднее оптимальное удержание рассчитывается как: с = Sj cj pj Где pj – веса соответствующие lj.С этим новым значением с мы возвращаемся к шагу 1. Правило остановки.Процесс останавливается как только будет достигнуто схождение. Мы не можем доказать сходимость, но на практике она должна иметь место. Заметим, что этот интуитивный результат может быть легко показан с помощью максимального правдоподобия:
Доказательство: Пусть x(1), x(2),…, x(k), c, x(k+1), …, x(n) будут порядковые статистики нашего наблюдения. Тогда логарифм правдоподобия (1) записывается:
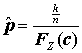 . .
Таким образом становится ясно, что доля p лиц, сообщающих обо всех страховых случаях, будет зависеть от параметрического распределения, выбранного для Z. Вкратце алгоритм выглядит так:Шаг 0. Инициализация. Выполнять:Шаг 1. Коррекция распределения размеров убытка. Максимизировать (1). Шаг 2. Корректировка частоты с/с. Для j = 1 до rПока не достигнута сходимость.Выполнять:Следующее j 8. Заключение. Изменение или введение BMS задача, которая может быть поставлена перед любой страховой компанией. В частности Бельгийские страховщики будут обязаны использовать новые BMS в связи с тем, что Европейская Директива запрещает использование единой BMS для всех водителей и для всех страховщиков.В этом случае возникает необходимость хотя бы иметь представление о реальных распределениях величины убытка и частоты страховых случаев, поскольку мы знаем, что на наши наблюдения воздействует “бонусный голод”. В этой работе дается решение проблемы получения оценок реальных распределений, путем использования непараметрической аппроксимации смесью Пуассоновских распределений и инверсии алгоритма Lemaire в отношении желания получить бонус. Также была определена доля страхователей, использующих алгоритм Lemaire для определения своего оптимального поведения. |