|
Библиотека Инструменты Все Страховщики Рейтинги Доп.Инфо Законодательство Ссылки. Советы Магазин Написать
|
2. Алгоритм Lemaire.
Алгоритм Lemaire (1977) требует следующих предположений:
- Пусть BMS состоит из s классов i = 0 …s–1.
- Частота убытков для отдельного страхователя имеет Пуассоновское распределение с параметром l.
- Величина выплаты есть X , а ее кумулятивная функция распределения -- FX (x).
- b – норма актуализации предсказаний в будущем.
- P
– полная премия, т.е. 100% базовой премии, включая рисковую надбавку, управленческие расходы, налоги и комиссии.
- 1 – t : 0 £ t < 1 есть время оставшееся до следующего внесения премии.
- m
– число страховых случаев, о которых сообщили компании за время [0, t ).
При этих гипотезах можно выполнить итеративный алгоритм, позволяющий водителю определить оптимальную для себя политику поведения в зависимости от бонусного класса к которому
он принадлежит. Оптимальная политика – просто оптимальное собственное удержание водителя как функция от уровня его бонусов. Т.е. уровень убытка до которого страхователю
выгодно оплатить убыток самому и не сообщать о нем страховщику. Разумеется, оптимальная политика также является функцией времени t, когда произошел страховой случай и
m , числа убытков о котором уже было сообщено страховщику до момента t , если конечно t не равно 0. Оптимальные частоты для водителя также определяются
данным алгоритмом.
Будет показано, что решение даваемое алгоритмом единственно при b < 1, что всегда верно, если процентные ставки положительны.
Короче говоря, алгоритм Lemaire дает водителю оптимальную частоту и оптимальное удержание, базирующиеся на реальных распределениях величины убытка и частоты страховых
случаев для данного водителя.
3. Непараметрическая аппроксимация смешанным Пуассоновским распределением.
Смешанное Пуассоновское распределение часто используется для моделирования числа выплат в автомобильном страховании.
Пусть П( k, t ) обозначает вероятность того, что риск порождает k убытков за t лет. По определению:
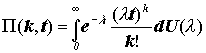
Классическими распределениями этого класса являются Отрицательное Биномиальное и Пуассоновское Инвертированное Гауссово.
В Walhin & Paris (1999) обсуждалась непараметрическая аппроксимация для П( k, t ). Мы напомним, что максимальное правдоподобие достигалось смесью нескольких
Пуассоновских распределений в зависимости от формы портфеля. Мы получили:
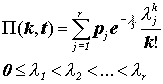
Если мы обозначим u максимальное число выплат приходящихся на риск, а v – число классов для которых наблюдения отличны от нуля, тогда при следующих условиях
существует единственное максимально правдоподобное решение:
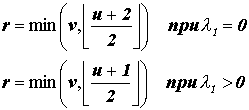
Для приведенного во введении примера мы получим:
Таблица 4. Максимально правдоподобные оценки параметров портфеля.
| l1 = 0,05461 | p1 = 0,56189 |
| l2 = 0,24599 | p2 = 0,41463 |
| l3 = 0,95618 | p3 = 0,02348 |
Эта аппроксимация дает интересную интерпретацию портфеля: Существуют 3 типа рисков lj , имеющих вероятности (веса)
pj .
4. Стационарное распределение страхователей по классам BMS.
При проведении наших вычислений мы будем предполагать, что BMS действует в течение длительного промежутка времени и что она достигла стационарного состояния (см. Lemaire (1995) ).
Пусть p(х) – вероятность того, что водитель со средней по системе частотой страховых случаев l вызывает х страховых случаев в течение
года. Тогда матрица перехода (Q) этого водителя из класса в класс внутри BMS, описанной во введении, будет такой:
Таблица 5. Матрица вероятностей перехода:
| s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | p(0) | 0 | 0 | p(1) | 0 | 0 | p(2) | 0 | 1 – p(0)– p(1)– p(2) |
| 1 | p(0) | 0 | 0 | 0 | p(1) | 0 | 0 | p(2) | 1 – p(0)– p(1)– p(2) |
| 2 | 0 | p(0) | 0 | 0 | 0 | p(1) | 0 | 0 | 1 – p(0)– p(1) |
| 3 | 0 | 0 | p(0) | 0 | 0 | 0 | p(1) | 0 | 1 – p(0)– p(1) |
| 4 | 0 | 0 | 0 | p(0) | 0 | 0 | 0 | p(1) | 1 – p(0)– p(1) |
| 5 | 0 | 0 | 0 | 0 | p(0) | 0 | 0 | 0 | 1 – p(0) |
| 6 | 0 | 0 | 0 | 0 | 0 | p(0) | 0 | 0 | 1 – p(0) |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | p(0) | 0 | 1 – p(0) |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | p(0) | 1 – p(0) |
|