Почему же инвесторы покупают катастрофические облигации? Спрос на ценные бумаги, основанные на страховом риске, может быть обоснован путем использования модели Markowitz’a. Как отмечалось выше, это модель финансового рынка, рассчитанная на один период времени. Доходы от активов в течение этого периода есть случайные величины R₁ , R₂ , … , R_n , с известными средними m_i = E R_i и S = [ s _{i j} ] где s _{i j} = Cov( R_i , R_j ).

Матрица S = [ s _{i j} ] , называемая матрицей ковариаций, в которой на диагонали расположены дисперсии переменных, имеет размерность n ´ n , является симметричной, и будем считать, имеет обратную к себе.

Портфель создается из п видов активов путем определения доли каждого актива в стоимости портфеля. Как и ранее мы предполагаем, что масштаб инвестиций не влияет на структуру портфеля, и инвесторы с одинаковыми рисковыми предпочтениями выберут одинаковые по структуре портфели. Поэтому для определения портфеля достаточно задать веса разных инвестиций. Как и ранее вес актива i обозначается w _i .

Доход от портфеля, обозначенного w^T = w₁, w₂, … w_n , есть R_w = S_{i=1 … n} w_i R_i . Таким образом доход портфеля – взвешенное среднее доходов отдельных ценных бумаг. Тогда доход ожидаемый от портфеля
m_w = E R_w и его дисперсия вычисляются, по весам инвестиций и их параметрам, следующим образом:

m_w = S i=1 … n w_i E R_i = m^T w
s²_w = S _{i=1 … n} w_i S i=1 … n w_j Cov( R_i , R_j ) = w^T S w

Таким образом дисперсия портфеля есть функция вектора весов и матрицы ковариаций.

По определению, эффективным является такой портфель ценных бумаг, над которым не доминирует никакой другой. Это портфель, для которого нельзя найти портфеля с меньшей дисперсией и с большим или равным доходом. На графике “ожидаемый доход – дисперсия” выше эффективного портфеля по вертикале нет ни одного другого портфеля; и слева по горизонтали также нет ни одного другого портфеля. Основная проблема при анализе портфелей – найти портфель с наименьшей дисперсией при заданном доходе или портфель с наибольшим доходом при заданной дисперсии. Оптимальным портфелем может быть только эффективный.

Существуют различные формулировки задачи оптимизации портфеля. Например, в [4] дана такая формулировка стандартной версии задачи: “При заданной требуемой инвестором доходности, r > 0 , и набора из п ценных бумаг, имеющих доходность m^T и матрицу ковариаций S определить вектор весов инвестиций w , который минимизирует дисперсию дохода s²_w = w^T S w при наличии двух ограничений:
S _{i=1 … n} w_i = 1 и m_w = m^T w = r .

Первое ограничение означает лишь то, что вся стоимость портфеля распределяется между выбранными п видами инвестиций. Для дальнейшего анализа будет удобно, если мы введем вектор e^T = [ 1, 1, …, 1 ]. Тогда первое ограничение переписывается в виде w^Te = 1. Второе ограничение требует, чтобы доходность портфеля была равна той, которую требует инвестор. Разумеется, существуют потенциально различные эффективные портфели, которые мы можем выбрать каждый для своей нормы доходности. Фактически, мы можем изобразить на графике весь набор эффективных портфелей, определяя точки графика (s_w , r ) путем решения портфельной задачи для различных значений s_w , соответствующих диапазону значений целевого ожидаемого дохода r. Этот график можно назвать эффективной границей для данных п активов. Эффективная граница может быть полностью определена в терминах двух эффективных портфелей. Это следует из “теоремы двух фондов” описанной в Luenberger [15, стр. 163] следующим образом.

Целевая функция, дополненная Лагранжевыми членами для ограничений имеет вид:

½ w^T S w + l( m^T w – r ) + n( w^Te – 1)

Здесь множитель ½ добавлен лишь для удобства. Целевая функция является квадратичной в отношении весов и линейной в отношении Лагранжевых множителей. Поэтому условия минимальности первого порядка дают систему из п+2 линейных уравнений:

S _{i=1 … n} w_j s _{i , j} + l m_i + n w_i = 0   для i = 1 … n
m^T w = r
w^Te = 1

Которую можно переписать в матричной форме:

S^Доп [ w , l , n ]^T = [ 0, …, 0 , r , 1 ]^T             (1)

Где S^Доп – результат дополнения матрицы S двумя строками и двумя столбцами:

В дополнение к обратимости матрицы S мы предположим, что вектор m не является прямо пропорциональным е. Это означает, что две последние колонки матрицы S^Доп линейно не зависимы. Ясно, что каждая из п первых колонок линейна независима от любой из двух последних. Из-за обратимости матрицы S первые п колонок линейно независимы между собой. Поэтому все колонки в матрице S^Доп линейно независимы и, следовательно, матрица имеет обратную к себе, а значит существует единственное решение (1) для вектора весов w и множителей l и n.

Пусть ( s_B , r_B ) обозначает риск и ожидаемый доход для портфеля, имеющего минимальную дисперсию. Этим мы указали эффективный портфель с минимальной дисперсией среди всех эффективных портфелей, имеющих различные значения r. В общем случае минимум дисперсии может быть равен нулю, что примерно соответствует рынку с безрисковыми инвестициями. Однако мы предположим, что здесь рассматриваются только рисковые активы и s_B > 0. Мы можем считать, что это портфель корпоративных облигаций, ибо они являются рискованными инструментами, но менее рискованными, чем акции. Пусть w_B , l_B , n_B обозначают соответствующие веса и мультипликаторы. Разумеется,

s_B = ((w_B )^T S w_B )^1/2 и m^T w_B = r_B.

Выберем некоторый другой эффективный портфель с параметрами w_S, l_S , n_S ; его ожидаемая доходность m^T w_S = r_S и риск s_S = ((w_S )^T S w_S )^1/2, причем r_S > r_B и s_S > s_B. Если, как мы договорились, ( s_B , r_B ) представляет собой портфель облигаций, то ( s_S , r_S ) есть портфель акций.

Возьмем некоторую точку на эффективной границе ( s, r ). Сформируем портфель с параметрами w , l , n удовлетворяющий уравнению:

[ w, l , n ] = (1 – a ) [ w_B , l_B , n_B ] + a [w_S , l_S , n_S ]

Здесь a = ( r – r_B ) / ( r_S – r ). Теперь, поскольку
S^Доп [w_B , l_B , n_B]^T = [ 0, …, 0 , r_B , 1 ]^T и S^Доп [w_S , l_S , n_S ]^T = [ 0, …, 0 , r_S , 1 ]^T,
то S^Доп [w , l₁ , l₂ ]^T = [ 0, …, 0 , r , 1 ]^T.

Поскольку решение уникально: r = m_w = (1 – a) r_B + a r_S и

s² = s²_w = D( (1 – a)R_B + a R_S ) =
(1 – a)² s ² _B + 2a(1 – a) r s² _B s² _S + a² s²_S

Здесь мы использовали для ковариации между двумя портфелями выражение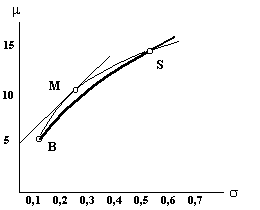
r s² _B s² _S , в котором соответственно r есть коэффициент корреляции. В результате, каждая точка на эффективной границе может быть представлена как линейная комбинация двух эффективных портфелей w_B и w_S . Этот вывод Luenberger и назвал “теоремой двух фондов”. Рисунок 6 иллюстрирует эту теорему. На нем отражены две возможные эффективные границы из которых более жирной линией изображена граница с большей корреляцией, а более тонкой – с меньшей. Это показывает, что, если ничего не изменяется, кроме корреляции, то эффективная граница сдвигается влево для всех точек между B и S.